Retroalimentación: una componente para la no-linealidad
Feedback: a component for non-linearity
Retroalimentación: una componente para la no-linealidad
Revista Jangwa Pana, vol. 19, núm. 3, pp. 476-492, 2020
Universidad del Magdalena

Esta obra está bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Recepción: 28 Junio 2019
Aprobación: 18 Agosto 2020
Resumen: Los paradigmas de la complejidad han tomado un ritmo acelerado en el uso de nuevos lenguajes y nuevos conceptos, implicando un nuevo paradigma y, como tal, un nuevo tipo de ciencia. La ciencia clásica trata de encerrar con un solo método y lenguaje todos los sistemas de comportamientos predecibles, regulares y controlables. El presente documento resalta un aspecto importante de los sistemas en complejidad: la no linealidad, . las retroalimentaciones como causa para ello. Los procesos iterativos o de retroalimentación en la interacción de las variables de un sistema son la mejor forma de describir el comportamiento global de los fenómenos, mostrando los procesos de causalidad circular, dejando a un lado la idea de causalidad lineal, es decir, la relación lineal unidireccional entre las causas y los efectos, y esta cadena de acciones genera en estos sistemas las emergencias. De este modo, se abre una ruta que transforme de la simplicidad a la complejidad y, por ende, de la disciplinariedad a la inter y/o transdisciplinariedad.
Palabras clave: bucles, causalidad, complejidad, fractales, linealidad, proceso iterativo.
Abstract: The paradigms of complexity have taken a fast pace in the use of new languages and concepts, implying a new paradigm and so, a new sort of science. Classic science tries to enclose in one method and language all predictable, regular and controllable behavior systems. This paper highlights a very important aspect in complexity systems: the non-lineary, and as cause of it, the feedback. The iterative or feedback processes in interaction with the variables of a system are the best way to describe the global behavior of phenomena, showing the circular processes of causality, setting aside the idea of linear causality, the one-way linear relationship between causes and effects, and the string of actions generated by this emergency systems. This way a route opens to transform from simplicity to complexity, and from disciplinary to inter or transdisplinarity.
Keywords: causality, complexity, fractals, iterative process, linearity, loop.
Introducción
“El todo es igual a la suma de sus partes”, a esto se reduce todo lo referente a la ciencia lineal. Stewart (citado en Longa. 2005) se refiere a la noción (de ciencia) lineal como una idea intrínseca de la predicción, es decir, en la ciencia lineal al realizar un mismo experimento reiteradamente, se obtendrá el mismo resultado en cada ejecución de este, y el acto de experimentar y corroborar los resultados a modo de observación lleva a pensar que cada componente, variable, parámetro y/o cualquier elemento del fenómeno en cuestión, dará un único resultado particular a base de su actuación; en otras palabras, se puede establecer la relación directa del elemento con el resultado final en el fenómeno. Este modo de razonar es el que se conoce como ciencia clásica, cuyo máximo exponente fue Isaac Newton, quien hizo grandes aportes con base en los trabajos de Kepler y Galileo. De aquí se inicia una forma de hacer ciencia: el determinismo, que consiste en que todo suceso está dado por una causa directa.
El determinismo ha contribuido con grandes descubrimientos que han dado un fuerte impulso al desarrollo del conocimiento, y estos avances también han contribuido a grandes descubrimientos para las ciencias. Sin embargo, no todo se conoce aún. Existen situaciones y/o fenómenos en la naturaleza y el universo que no se han podido conocer de manera detallada. Tales lagunas en el conocimiento tienen una motivación que proviene del mismo determinismo.
La visión mecánico newtoniana se basa en tres rasgos (García, Mateos, Olmedo, 2005, p. 80):
- 1. El positivismo, entendido como una corriente que asegura que el conocimiento viene dado por la experiencia.
- 2. Relación lineal causa-efecto.
- 3. El reduccionismo, que postula la acción de simplificar como algo necesario para resolver problemas.
Esto conduce a una “simplificación” de la realidad, es decir, reduce, en todo el sentido de la palabra, el fenómeno o situación por describir, a unas cuantas componentes estructurales, cuyas relaciones sean tan simples como lo indique la experiencia en trabajos anteriores. En pocas palabras, un “paradigma de simplicidad” gobernado por la disyunción, que consiste en separar realidades que están estrechamente relacionadas y la reducción.
Tal paradigma está fundamentado, constructivamente, por tres procesos (Scott, 2007):
- 1. Análisis: consiste en la explicación a nivel superior, por componentes separadas que se estudian individualmente.
- 2. Formulación: obtención del modelado e interacción de sus componentes.
- 3. Síntesis: derivar y comparar el fenómeno a nivel superior, cuantitativamente, con observaciones empíricas.
Cabe aclarar que el análisis y la síntesis corresponden a una direccionalidad “reduccionista” descendente (de nivel superior a nivel inferior), y ascendente (de nivel inferior a nivel superior), respectivamente (Longa, 2005).
El reduccionismo es la principal causa de la ausencia de un total conocimiento, ya que poner límites a la cuestión en estudio lleva inevitablemente a un grado de incertidumbre en la comprensión neta del fenómeno.
Contrariamente, la teoría de sistemas propone no delimitar la situación, o lo que es lo mismo, no imponer fronteras, dará mayor claridad en la descripción. En efecto, considerar el fenómeno como un sistema (unidad total interrelacionada) permitirá trascender en la búsqueda del saber.
Luz Ramírez (2002) retoma (de Johanzen,4Von Bertalanffy,5 Khandwalla,6 Miermont7 y otros) algunas definiciones para el concepto de sistema, las cuales, básicamente, difieren en el énfasis que se le aplique:
-
Conjunto de partes coordinadas y en interacción para alcanzar un objetivo.
-
Grupo de partes que interactúan bajo las influencias de fuerzas en alguna interacción definida.
-
Totalidad distinguible en un entorno o ambiente en el cual interactúa, compuesta a su vez de elementos que interactúan también.
-
Todo aquello que tiene un objetivo.
-
Grupo de unidades combinadas que forman un todo organizado.
-
Un todo integrado cuyas propiedades esenciales surgen de las relaciones entre sus partes.
-
Un grupo de componentes interrelacionados que trabajan en conjunto hacia una meta común mediante la aceptación de entradas y generando salidas en un proceso de transformación organizado.

Estos rasgos estructurales y funcionales, al tenerlos en cuenta, impiden el parcelamiento y/o reduccionismo del sistema (Flórez, Thomas, 1993, pp. 126-127).
Por otro lado, hablar de complejidad no se refiere ya a una ciencia como control o de manipulación, sino a sistemas y fenómenos que se adaptan, con comportamientos irreversibles y aperiódicos. Carlos Maldonado (2014) afirma que la ciencia hoy día no parte ni trabaja con definiciones y, por el contrario, parten y trabajan con problemas. En este tipo de ciencia, los sistemas y/o comportamientos son no lineales y emergentes, y su característica esencial son los procesos de retroalimentación. Por ello, el presente artículo realza los procesos iterativos o de retroalimentación en la interacción de las componentes de un modelado, cuestionando la bidireccionalidad entre la relación entre causa y efecto. Para ello, se presenta en primer lugar la idea de linealidad en términos matemáticos, seguidamente se alude a lo que se entiende por causalidad y retroalimentación. En segundo lugar, se enmarcan los procesos iterativos para destacar los sistemas dinámicos continuos y discretos. Posteriormente se presenta la no linealidad como una particularidad de los sistemas en complejidad, haciendo un paralelo entre linealidad y no linealidad.
Linealidad
En matemáticas, cuando se habla de “linealidad” o “ser lineal”, inmediatamente se hace alusión a una proporcionalidad directa.
En el caso de la geometría (euclidiana), figura el teorema de Tales de Mileto, que explica la construcción de un triángulo semejante a uno dado. “Si tenemos dos rectas 𝑟 y 𝑠 de un plano, tres rectas paralelas entre sí que corten a las anteriores, determinan segmentos correspondientes proporcionales” (Gallego, Linares, 1988, p. 76). Es decir que, si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado:
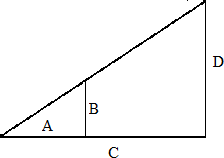
Figura 1.
Semejanza entre dos triángulos.
Esta idea de “linealidad” se extiende a espacios abstractos matemáticos más generales, como lo son el operador lineal y el funcional lineal.
Operador lineal
En análisis funcional, un operador 𝑇 entre espacios vectoriales, se dice lineal cuando satisface las siguientes condiciones (Kreyszig, 1978):
- 1. El dominio 𝐷(𝑇) de 𝑇 es un espacio vectorial y el rango 𝑅(𝑇) se encuentra en un espacio vectorial sobre el mismo campo.
- 2. Para todas las 𝑥, 𝑦 ∈ 𝐷(𝑇) y escalares 𝑎, se satisface 𝑇(𝑥 + 𝑦) = 𝑇(𝑥) + 𝑇(𝑦), y 𝑇(𝑎𝑥) = 𝑎𝑇(𝑥)
Por ejemplo, la función 𝑓: ℝ2 → ℝ3 definida por 𝑓(𝑥, 𝑦) = (𝑥 + 𝑦, 𝑥 − 𝑦 3𝑥) es lineal. En efecto, dados 𝑎, 𝑏 ∈ ℝ, 𝑋 e 𝑌 en ℝ2, se verifica 𝑓(𝑎 ∗ 𝑋 + 𝑏 ∗ 𝑌) = 𝑎 ∗ 𝑓(𝑋) + 𝑏 ∗ 𝑓(𝑌). En palabras menos técnicas, un operador lineal es aquella transformación que preserva las operaciones de los espacios (Campos, Pérez, Villamarín, Garzón, Mora. 2004, p. 41).
Funcional lineal
Un funcional lineal es un operador lineal con dominio un espacio vectorial 𝑋, y rango el campo o cuerpo 𝐾 de 𝑋, esto es, 𝑓: 𝐷(𝑋) → 𝐾, donde 𝐾 = ℝ, o ℂ.
Causalidad
Si bien se sabe que toda acción genera otra acción, entonces se puede decir qué evento/suceso/acción fue el/la responsable/causa para que se origine/efectúe cierta acción. De eso trata la causalidad.
La causalidad se asimila de una manera simple, haciéndose la pregunta ¿de dónde viene tal cosa? o simplemente, ¿por qué se originó tal cosa? Es decir, es tratar de comprender la causa por la cual se originó cierto efecto, y estas pueden estar motivadas de diferentes maneras (Scott, 2007, p. 282):
-
Causa material: hace referencia al promedio de tiempo o espacio sobre las variables dinámicas en niveles bajos, y estas variables ingresan como un parámetro que varía muy lentamente hasta llegar al nivel de interés.
-
Causa formal: hace referencia a la organización con que se da el efecto, es decir, a las condiciones de frontera en el nivel de interés.
-
Causa eficiente: hace referencia al estímulo-respuesta, a la respuesta del término al cual se forzó para la obtención de una respuesta.
-
Causa final: hace referencia simplemente a la intencionalidad con que se realiza la causa, la intención de lograr cierto efecto.
Esto da lugar a cuando un objeto tiene la capacidad o no, de ejercer ciertas causas a partir de sus propiedades. Esto se conoce como el principio del poder causal:
Para que un objeto 𝑋 ejerza en el tiempo 𝑡 los poderes causales/determinativos que tiene en virtud de poseer la propiedad 𝑃, 𝑋 ya debe poseer 𝑃 en 𝑡. Cuando se provoca que 𝑋 adquiera 𝑃 en 𝑡, es decir, 𝑋 no posee 𝑃 en 𝑡, inmediatamente 𝑋 no es capaz de ejercer los poderes causales/determinativos inherentes en 𝑃. (Scott, 2017, p. 287).
Causalidad lineal y no lineal
Supongamos que 𝐴1 causa 𝐵1, y 𝐴2 causa 𝐵2, es decir,
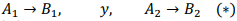
Una relación lineal estaría dada por 𝐴1 + 𝐴2 → 𝐶 = 𝐵1 + 𝐵2, es decir, el efecto total 𝐶 que resulta de las causas 𝐴1, 𝐴2 se puede separar en dos efectos independientes 𝐵1, 𝐵2. En términos clásicos, el todo igual a la suma de las partes.
De otro lado, si 𝐶 ≠ 𝐵1 + 𝐵2, se dice que hay una respuesta no lineal a las causas.
En general, (∗) se puede extender, al dividir arbitrariamente 𝐴 en componentes (𝐴1, 𝐴2, 𝐴3, … , 𝐴𝑛) con lo que el efecto se dividirá, correspondientemente en (𝐵1, 𝐵2, 𝐵3, … , 𝐵𝑛).
Retroalimentaciones
En la dinámica de sistemas (estudio de los sistemas complejos enfocado en los bucles o ciclos de alimentación) o mejor (técnica de simulación de los sistemas complejos donde se describen los sistemas en términos de cadenas de retroalimentación), existen los diagramas de bucle causal, que conecta con un vínculo causal la variable causante con la variable afectada. En un diagrama, esto es:
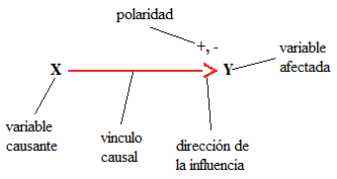
Figura 2.
Diagrama causal.
La polaridad del vínculo causal indica el efecto que ofrece la variable causante cuando esta evoluciona, es decir, es la relación de los signos entre el evento y el efecto (Schaffernicht, 2006); por ejemplo: a mayor publicidad, mayores serán las ventas; o, a más muertes, menor será la población. Para estos casos la polaridad del vínculo causal será positiva y negativa, respectivamente.
Se puede esperar que la variable afectada influya, de algún modo, en la variable causante, es decir, “cuando la causalidad es tal que el cambio de una determinada variable vuelve a incidir en esta misma variable, hablamos de retroalimentación” (Schaffernicht, 2006, p. 134). Gráficamente:

Figura 3.
Diagrama de bucle causal.
Para Jay Forrester, es una percepción errónea creer que la causa y el efecto fluyen unidireccionalmente, ya que siempre se habla de que la acción A motiva la acción B, y esta noción unidireccional es incompleta, pues el efecto B genera o representa una nueva condición del sistema que puede dar lugar a influencias en el futuro que afectan o alteran la acción de A. Así mismo, entre los tres principios de pensamiento complejo que plantean Morin, Ciurana y Mota (2002, p. 30) se encuentra el recursivo, que afirma que se debe romper con la linealidad de causa-efecto puesto que los efectos pueden ser las causas y/o viceversa. Cabe resaltar las propiedades que caracterizan la relación lineal tradicional causa–efecto citado en (Izquierdo, Galán, Santos y Del Olmo, 2008):
- 1. La causa precede al efecto en el tiempo.
- 2. Existe una fuerte correlación empírica entre causa y efecto.
- 3. Esta relación no es resultado de ninguna otra variable.
Estos “bucles de retroalimentación” constituyen el concepto más importante para establecer la estructura de un sistema, pues “el circuito de retroalimentación es el camino cerrado que conecta una acción con su efecto sobre la condición circundante, y estas condiciones resultantes a su vez regresan como información para influir en la acción futura” (Forrester, 1971, p. 17).
En los procesos de retroalimentación, la información suministrada sobre las acciones en curso nutre al sistema, realimentándolo, permitiendo describir comportamientos orientados para un fin. Esto se conoce como bucles de causalidad circular, diferentes de los procesos de causalidad lineal (Reynoso, 2006).
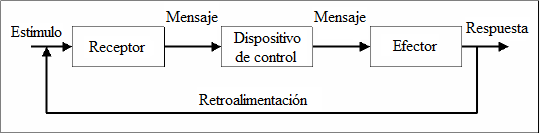
Figura 3.
Diagrama de retroalimentación. (Tomado de Reynoso, 2006).
Las retroalimentaciones pueden ser (Schaffernicht, 2006):
-
Positivas
-
Negativas
-
Oscilación
-
Crecimiento en “S”
-
Sobre-reacción
-
Auge y derrumbe
Los feedback poseen dos variables, los niveles que actúan como acumuladores en el sistema, y las tasas de flujos que hacen que los niveles cambien. Estas dos variables son necesarias y suficientes, y sin importar qué tan simple sea el feedback o bucle de retroalimentación, este debe contener una variable de cada una como mínimo (Forrester, 1969, 1971).
Por ejemplo, en los bucles de retroalimentación positiva las relaciones son en su totalidad del mismo signo, por lo que hace que aumenten constantemente el crecimiento de las variables, y, por el contrario, en los bucles de retroalimentación negativa algunas relaciones son de diferente signo y esto hace que el sistema tienda a equilibrase. Un ejemplo de estos bucles lo muestra (Sonnessa, s.f.):
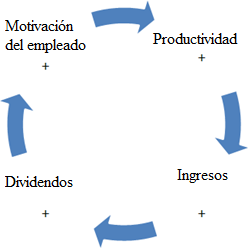
Figura 4.
Bucle de retroalimentación positiva. (Tomado de Sonnessa, s.f.)
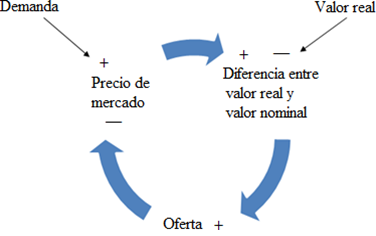
Figura 5.
Bucle de retroalimentación negativa. (Tomado de Sonnessa, s.f.)
Esta interacción entre agentes (variables del sistema) hace surgir una complejidad dinámica a largo plazo, es decir, una interacción entre bucles entre sí está motivada por redes de retroalimentación positivas y negativas,8 siendo estas redes un rasgo estructural para todos los sistemas, sin importar qué tan complejos sean, complejidad que depende precisamente de dichas interacciones (bucles y redes de bucles) de las componentes, y no de la complejidad de las componentes (Sterman, 2000). Según (Izquierdo, Galán, Santos y Del Olmo, 2008), la identificación de las relaciones de causalidad entre las variables de los sistemas complejos hace mucho más fácil la explicación del origen de comportamientos globales del sistema, es decir, descripciones a partir de su estructura causal.
El papel que cumple el feedback en la transformación de la metodología simplista del estudio de un sistema a una metodología compleja, viene dado por la siguiente línea (García, Mateos, Olmedo, 2005):
-
Primeramente, una organización cerrada (limitada): es el mismo paradigma de la ciencia clásica, pues limita el fenómeno a unas cuantas componentes con sus relaciones más relevantes, ignorando aquellas que, de manera implícita o muy débil, también influyen en el sistema. Los límites impuestos mediante este pensamiento logran un control ajustado y una descontextualización, implicando una “ritualización” metodológica, es decir, hacer siempre lo mismo que se hizo antes. Todo este proceso de indagación y entendimiento del sistema solo busca una adaptación del presente para el futuro que se llega a predecir.
-
Proceso aleatorio o estadístico: en esta etapa la incertidumbre, que se puede entender como la falta de previsión de un suceso, ha aumentado, pero, aun así, es posible predecir con base en las situaciones actuales. Las relaciones entre las componentes siguen siendo deterministas, con la diferencia de que ahora lo están en términos aleatorios.
-
Proceso a la complejidad: aquí la incertidumbre es impredecible. Las relaciones causa- efecto dejan de ser determinables, aumentando y/u obteniendo ganancia de información, debido a los procesos de retroalimentación positiva.
Esto indica que la acción de retroalimentar es propia de los sistemas de la complejidad, ya que son sistemas caracterizados por el no equilibro (alejados del equilibrio), relaciones no lineales, no periodicidad, la irreversibilidad y propiedades emergentes. Cabe destacar que los sistemas complejos no son deterministas (el pasado determina el presente), y por el contrario, el pasado es cualitativamente diferente al futuro, la complejidad de los sistemas radica en que sus dinámicas y estructuras no pueden ser reducidas a explicaciones regulares, periódicas y previsibles (Maldonado, 2014). En efecto, la distinción entre un sistema complicado (sistema compuesto por muchos sistemas simples) y un sistema complejo, son las emergencias (resultados no observables a nivel microscópico), y es lo que hace que el todo sea más que la suma de las partes.
La visión de Chris Langton (Lewin, 1992, p. 27) acerca de las emergencias es una interacción de los resultados globales no previstos a nivel local pero que influyen en la interacción local; en otras palabras, “la idea establece que las características del todo no pueden deducirse a partir de las características de las partes” (Reynoso, 2006, p. 26). De igual forma, enfatiza que las totalidades complejas se originan en principios y elementos muy simples, esto es, gráficamente:
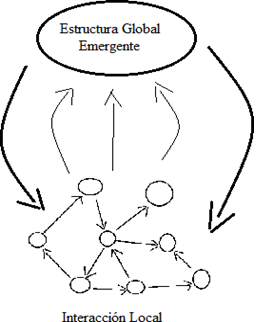
Figura 6.
Visión de Langton de la emergencia de los sistemas complejos.
Procesos iterativos
Son aquellos en los que se repite la misma acción para lograr algún objetivo dado. En matemáticas, los procesos más conocidos son los que se dan en los sistemas dinámicos.
Sistemas dinámicos
Un sistema dinámico es un modelo matemático utilizado para estudiar procesos iterativos de naturaleza determinista o aleatoria (Montealegre, Londoño y Polanía, 2002, p. 63). Todo proceso ocurre en su propio tiempo, que puede ser discreto o continuo. El proceso está caracterizado por variables y/o parámetros, los cuales interactúan mediante relaciones funcionales (lineales o no lineales).
Formalmente, un sistema dinámico es un par (𝑀, 𝐹) donde 𝑀 representa el espacio temporal, es decir, el ambiente del sistema, llamado espacio de estados o espacio de fases.
𝐹 es una aplicación del espacio de estados en él mismo 𝐹: 𝑀 → 𝑀 y esto ocurre gracias a la llamada ley de evolución del sistema o ley de transición de estados. El conjunto 𝑀 generalmente es una vecindad diferenciable (Montealegre, Londoño y Polanía, 2002).
Sistemas dinámicos continuos
Si el sistema dinámico es continuo, la aplicación F es un campo vectorial, definido por el lado derecho de un sistema de ecuaciones diferenciales:
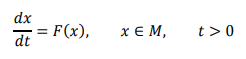
Los ejemplos más usuales son los sistemas de ecuaciones diferenciales, cuyas aplicaciones son diversas (Polanía, 2011).
Sistemas dinámicos discretos
Si el sistema dinámico es discreto, 𝐹 generalmente es un difeomorfismo (una función diferenciable con inversa diferenciable); el sistema dinámico se expresa mediante una ecuación en diferencias de la forma:
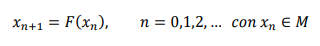
Aquí se genera una sucesión de iterados, donde el término siguiente está en función del término inmediatamente anterior. Un ejemplo peculiar es el método iterativo de Newton, algoritmo iterativo que permite calcular las raíces de una función (usualmente no lineal) a partir de una buena aproximación a dicha raíz.
Ejemplos clásicos
-
El conjunto ternario de Cantor. Fue creado por George Cantor, y se construye extrayendo el tercio medio abierto de un segmento de recta de longitud finita, repitiendo el mismo proceso para los dos segmentos de recta restantes, y así sucesivamente; en forma gráfica esto es:
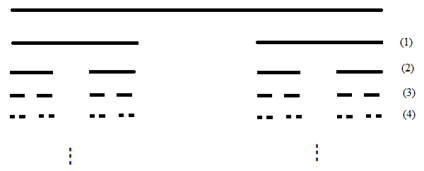
Figura 7.
Conjunto ternario de Cantor.
Este proceso es llevado hacia el límite, es decir, el conjunto de Cantor es el objeto que queda al final luego de aplicar reiteradamente la extracción del intervalo medio abierto.
-
La curva de Koch. Fue creada por N. F. Helge von Koch; a diferencia del conjunto de Cantor, esta curva se obtiene añadiendo segmento de recta a un segmento inicial, lo cual hace que al final obtengamos una curva; esto es:
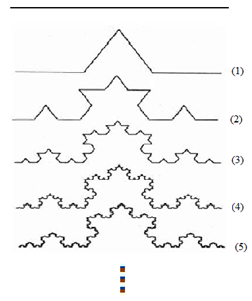
Figura 8.
Curva de Koch.
-
El triángulo de Sierpinski: Creado por Waclaw Sierpinski. Es análogo al conjunto de Cantor, y se obtiene por una sucesión infinita de extracciones; esto es:
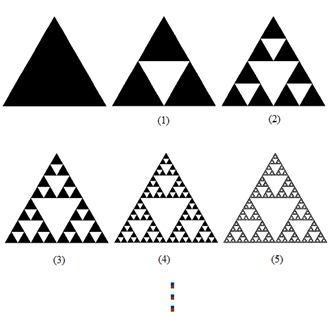
Figura 9.
Triángulo de Sierpinski.
De los anteriores ejemplos, lo más importante es resaltar la pérdida de dimensión entera que sufren estos objetos iniciales al ser transformados por un proceso iterativo llevado al infinito. En efecto, para el conjunto ternario de Cantor, el objeto inicial (segmento de línea recta-dimensión 1) pasa a una polvareda de puntos que no es de dimensión cero, más exactamente .En la curva de Koch, el segmento de línea recta inicial se transforma en una curva de longitud infinita a pesar de que la rodea un área finita, y su dimensión es . En el triángulo de Sierpinski, el triángulo inicial (dimensión 2) se transforma, análogamente al conjunto de Cantor, en una polvareda de puntos, y su dimensión es (Rubiano, 2011, p. 22).
Estos conjuntos que se logran por transformaciones mediante un proceso iterativo llevado al infinito crean una estructura fractal,9 es decir, conjuntos que poseen autosimilitud a una escala menor y una dimensión no entera. Lo que evidencia algunos principios del pensamiento complejo (Morin, Ciurana, Mota, 2002); el principio de recursividad (la acción de iterar), el principio dialógico, lógicas que se complementan y se excluyen -la fractalidad es una forma de evidenciar el caos (diálogo entre orden y desorden)-, y el principio hologramático (el todo está en la parte que está en el todo, o simplemente, autosimilitud a escala).
No linealidad
La no linealidad es simplemente la ausencia de linealidad, y está caracterizada por las emergencias, causantes de una “imposibilidad de predicción determinista” (Sotolongo, 2007, p. 16). Es decir, cuando pasamos de la linealidad a la no linealidad es lo mismo que pasar de la predictibilidad a la impredictibilidad. Según Maldonado (2015) este cambio viene dado por dos casos:
El primero es, cuándo y cómo un sistema lineal se convierte en uno no-lineal, y es gracias a las contribuciones más clásicas que provienen del caos y, más recientemente, de las redes complejas; o bien, cuándo y cómo un sistema lineal puede ser transformado en uno no-lineal, y dicha transformación de un fenómeno lineal en uno no-lineal es, en términos matemáticos, una transformación geométrica. (p. 415).
En el primer caso, tiene como motivación el estudio de sistemas (no lineales) que poseen propiedades derivadas a partir de las condiciones iniciales, y llevan a ser impredecibles sistemas que son muy simples. Este estudio da como germen la teoría del caos, entrando en contacto con la teoría de bifurcaciones y la teoría de catástrofes. Aquí algunas definiciones para el término “caos” (Curras. 1995, p. 15):
-
Comportamiento recurrente, en apariencia debido al azar, en un sistema determinista (H. Bruce Stewart).
-
Órbitas complicadas, aperiódicas y atractivas, de ciertos sistemas dinámicos (Philip Holmes).
-
Un sueño… donde se presentan sistemas de cadenas de posiciones de orden y predictibilidad en situación dinámica libre (Joseph Ford).
-
Clase ubicua y recientemente conocida, de fenómenos naturales (Hao Bai-Lin).
-
Comportamiento que produce información (James Crutchfield).
-
Salva las fronteras de las disciplinas científicas (Michell Feigenbaum).
-
Un fenómeno, producido en un lugar, trasmite información, que se propaga en el espacio y repercute en la observación de otro fenómeno, de mayor magnitud en un lugar distante (Edward Lorenz).
Para el segundo caso, proviene de pensar geométricamente, es decir, después del álgebra (siglos XVII y XVIII) y del cálculo (siglos XVIII y XIX), la geometría fue la vencedora de las matemáticas en el siglo XX, “desde la topología, fundada por Poincaré (reconociendo la obra de Smale), importantes desarrollos posteriores se harán posibles, como la teoría de catástrofes de Thom, la geometría fractal de Mandelbrot, la teoría del caos de Lorenz, en fin” (Maldonado, 2011, pp. 128-129).
Linealidad vs no-linealidad
Cualitativamente, en matemáticas los retratos de fases de un sistema de ecuaciones diferenciales nos brindan información acerca del comportamiento de las soluciones de dichos sistemas. El teorema de Hartman-Grobman, establece que, en una vecindad del punto de equilibrio hiperbólico del sistema, los retratos de fases entre el sistema no lineal y el mismo sistema linealizado son topológicamente equivalentes, es decir, los retratos de fases del sistemas lineal y no lineal muy cerca del punto de equilibrio son similares. Por ejemplo, sea el sistema no lineal
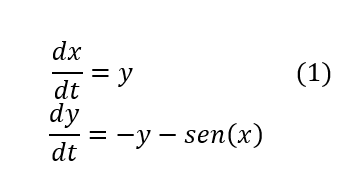
El retrato de fase para el sistema (1) es el siguiente:
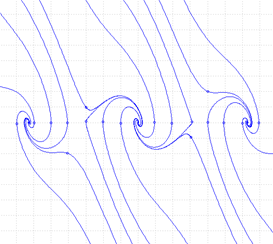
Figura 10.
Retrato de fases para el sistema no lineal (1).
Una vez linealizado el sistema (1), nos queda de la siguiente forma:
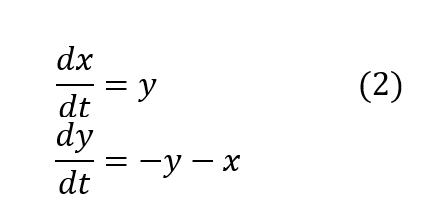
Y el retrato de fases será:
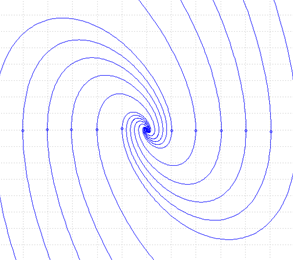
Figura 11.
Retrato de fases para el sistema (1) linealizado.
Nótese la gran diferencia entre los retratos de fases. En la figura 10 resaltan más de un punto de equilibrio, esto se debe a la periodicidad de la función seno, caso contrario al de la figura 11, ya que con la linealización del sistema se pierde dicha periodicidad, resultando solo un punto de equilibrio.
Conclusiones
En los paradigmas de la complejidad, la no-linealidad es una característica propia de esta ciencia y, por tanto, no se puede quitar la esencia a los sistemas en complejidad, porque entonces ya no existiría ninguna complejidad. Sin embargo, en la ciencia clásica existen métodos analíticos que consisten en la linealización de la no-linealidad y esto funciona como sinónimo de reduccionismo y simplificación de los fenómenos, lo que implica inevitablemente pérdida de información. Respecto a esto, y en concordancia con varios autores, se afirma que un fenómeno no-lineal se caracteriza principalmente porque gana información y no necesariamente memoria; por tanto, se subraya que la no-linealidad y la ganancia de información son mutuamente complementarias.
Por otro lado, imponer la relación causa-efecto de manera lineal impide prever las pequeñas relaciones que, de manera minúscula, también aportan un esfuerzo necesario y suficiente para generar el resultado final. Los bucles de causalidad circular alimentan al sistema, nutriendo información, con el objetivo de describir los comportamientos globales de los fenómenos a partir de su causalidad. Con base en esto, la complejidad de los fenómenos o sistemas depende exclusivamente de las interacciones de sus componentes. Además, los bucles causales o la acción de retroalimentar es un acto propio de los sistemas de la complejidad y son las principales causas de las emergencias en estos sistemas, puesto que gracias a que el efecto producido incide en la causa, impulsa al sistema o a la variable determinada producir resultados no esperados.
Referencias
Bertalanffy, L. (1976). Teoría General de los Sistemas. Madrid: Fondo de Cultura económica.
Campos, M.; Pérez, J. De Villamarín, G. Garzón, M., y Mora, C. (2004), Fundamentos de Álgebra Lineal. Bogotá: Pro-Offset Editorial Ltda.
Braun, E. (1996). Caos, Fractales, y Cosas Raras. México: Fondo de Cultura Económica.
Curras, E. (1995). Caos y orden en la organización del conocimiento. Organización del conocimiento en sistemas de información y documentación: actas del II Encuentro de ISKO-España. Getafe, 16 y 17 de noviembre de 1995. Madrid. España.
Forrester, J. (1969). Urban Dynamics. Cambridge, Massachusetts: Pegasus Communications, Inc.
Forrester, J. (1971). World Dynamics. Cambridge, Massachusetts: Wright-Allen Press, Inc.
García, J.; Mateos, R. y Olmedo, E. (2005). De la Linealidad a la Complejidad: Hacia un Nuevo paradigma. España: Cuadernos de Estudios Empresariales.
Gallego, J. y Linares, F. (1988). Teorema de Tales. Números. Revista de Didáctica de las Matemáticas, 18, 71-76.
Flórez, A. y Thomas, J. (1993). La teoría general de sistemas. Cuadernos de Geografía: Revista Colombiana de Geografía, ISSN 0121-215X, ISSN-e 2256-5442, Vol. 4, Nº. 1-2, 111-137.
Izquierdo, L.; Galán, J.; Santos, J. y Del Olmo, R. (2008), Modelado de sistemas complejos mediante simulación basada en agentes y mediante dinámica de sistemas. EMPIRIA. Revista de Metodología de Ciencias Sociales, 16.
Johansen, O. (1982). Introducción a la teoría general de sistemas. Editorial Limusa.
Khandwalla, PN. (1974). Administrative Science Quarterly. SAGE JOURNAL.
Kreyszig, E. (1978), Introductory Functional Analysis with Applications, John Wiley & Sons. Inc. Canada.
Lewin, R. (1992), Complejidad. El caos como generador de orden. Barcelona: Tusques Editores.
Longa, M. (2005). Filosofía de la ciencia y la ciencia no lineal. España. Revista Teorema, Vol. XXIV/1.
Maldonado, C. (2011), Termodinámica y Complejidad. Una introducción para las ciencias sociales y humanas. Bogotá: Ediciones desde abajo.
Maldonado, C. (2014). ¿Qué es un sistema complejo? Revista Colombiana de Filosofía de la ciencia. Vol. 14, 29.
Maldonado, C. (2015), Transformación de la no-complejidad a la complejidad. Revista INGENIERÍA, Vol. 21, No. 3.
Montealegre, M.: Londoño, G. y Polanía, A. (2002). Fundamentos de los Sistemas Dinámicos: La interdisciplinariedad desde los Sistemas No lineales. Neiva: Universidad Surcolombiana.
Miermont, J. (2001). Dictionnaire des thérapies familiales. Payot.
Morin, E.; Ciurana, E. y Mota, R. (2002). Educar en la era planetaria. Barcelona: Gedisa S. A.
Polanía, L. (2011), Un enfoque cualitativo de las EDO’s y Teoría Wavelets, Neiva: Universidad Surcolombiana.
Ramírez, L. (2002). Teoría de Sistemas. Manizales: Universidad Nacional de Colombia, Sede Manizales.
Reynoso, C. (2006). Complejidad y el Caos: Una exploración antropológica. Universidad de Buenos Aires.
Rubiano, G. (2011). Iteración y Fractales (con Mathematica). Primera ed. Editorial Universidad Nacional de Colombia. Bogotá, D.C. Colombia.
Schaffernicht, M. (2006). Indagación de situaciones dinámicas mediante la Dinámica de sistemas. Editorial Universidad de Talca.
Scott, A. (2007). THE NONLINEAR UNIVERSE. Chaos, Emergency, Life. Springer-Verlag Berlin Heidelberg.
Sonnesa, M. (s.f.) Modelling and simulation of complex systems.
Sotolongo, P. (2007). Complejidad, no linealidad, y redes distribuidas. Revista COMPLEXUS.
Sterman, J. (2000). Business Dynamics. Systems Thinking and Modeling for a Complex World. MIT. McGraw-Hill.
Notas
Notas de autor
Información adicional
Cómo citar este artículo: Ovalle Cerquera, D. E.; Polanía Quiza, L. A., y Rodríguez Rodríguez, J. (2020). Retroalimentación: Una componente para la no-linealidad. Jangwa Pana, 19(3), 476 - 492.
